JAKARTA, incaschool.sch.id – Algebra: Solving Equations and Understanding Relationships always felt intimidating to me during school days. I remember staring at those x’s and y’s, thinking, “What even is this?” But turns out, it’s a whole lot more practical than we’re told. Here’s what I’ve figured out after years of stickin’ with it (and trust me, making loads of mistakes!).
Algebra is a key branch of mathematics that studies symbols and the rules for operating on them. It serves as a powerful tool for solving equations and understanding relationships, making it essential for both academic success and real-life applications. This article explores the key concepts of algebra, the importance of solving equations, and how these skills can lead to real-life wins.
1. Understanding Algebra
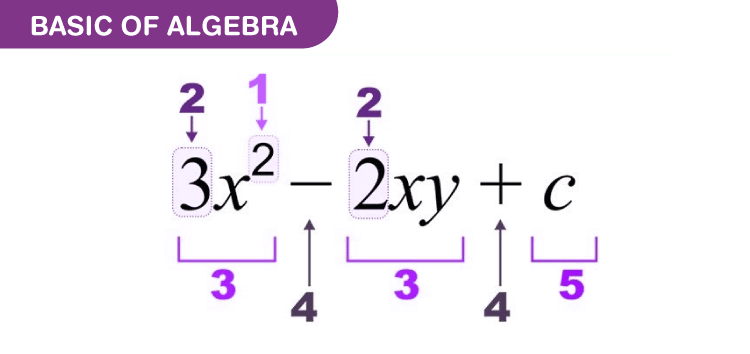
At its core, algebra involves using letters (variables) to represent numbers in equations and expressions. This allows for the formulation of general rules and relationships that can be applied to various situations.
– Key Components of Algebra
- Variables: Symbols (often letters like x, y, or z) that represent unknown values.
- Constants: Fixed values that do not change (e.g., 3, −5).
- Expressions: Combinations of variables and constants using mathematical operations (e.g., 2x+3).
- Equations: Mathematical statements that assert the equality of two expressions (e.g., 2x+3=7).
2. The Importance of Solving Equations
Solving equations is a fundamental skill in algebra that enables individuals to find unknown values and make informed decisions based on mathematical relationships.
– Real-Life Applications
- Finance: Algebra is used to calculate budgets, loans, and investments. For example, if you want to determine how much you need to save monthly to reach a financial goal, you can set up an equation based on your savings plan.
- Science and Engineering: Many scientific formulas rely on algebraic equations. For instance, calculating the trajectory of a projectile involves solving equations that describe its motion.
- Everyday Situations: From determining the best price for products to adjusting recipes, algebra helps in solving everyday problems efficiently.
3. Solving Linear Equations
One of the most common types of equations in algebra is the linear equation, which can be expressed in the form ax+b=c, where a, b, and c are constants.
– Steps to Solve a Linear Equation
- Isolate the Variable: Use inverse operations to get the variable by itself on one side of the equation.
- Divide or Multiply: If the variable is multiplied by a coefficient, divide both sides by that coefficient.
- Check Your Solution: Substitute the value back into the original equation to verify correctness.
4. Understanding Relationships with Algebra
Algebra is not just about solving equations; it also helps in understanding relationships between variables. This is often represented through functions.
– Functions and Graphing
- Definition of a Function: In a function, every input (independent variable) yields one—and only one—output (dependent variable).
- Graphing Functions: Graphing allows you to visualize the relationship between variables. The horizontal axis denotes the independent variable, and the vertical axis denotes the dependent variable.
– Real-Life Relationships
- Proportions: Algebra helps in understanding proportions, such as the relationship between distance, speed, and time. The equation d=rt (distance = rate × time) illustrates this relationship.
- Comparative Analysis: Algebra can help compare different scenarios. For instance, if you want to compare the cost of two different mobile plans, you can set up equations to determine which is more economical based on usage.
5. Quadratic Equations and Their Applications
Quadratic equations, in the form ax2+bx+c=0, are another critical area of algebra.
– Solving Quadratic Equations
- Factoring: If possible, factor the equation to find the roots.
- Quadratic Formula: If factoring is not feasible, use the quadratic formula: x=−b±b2−4ac2a
- Graphing: The graph of a quadratic equation is a parabola. Understanding the vertex and intercepts can provide insights into real-world scenarios, such as projectile motion.
6. Conclusion
In conclusion, algebra is a powerful tool that enables individuals to solve equations and understand relationships in various contexts. Mastering algebraic concepts not only enhances academic performance but also equips students with essential problem-solving skills applicable in everyday life. Whether calculating finances, analyzing data, or making informed decisions, algebra serves as a foundation for achieving real-life wins. By embracing the principles of algebra, students can unlock new opportunities and navigate the complexities of the world around them with confidence.
Explore our “Knowledge” category for more insightful content!
Don't forget to check out our previous article: Tips to Study: Strategies for Academic Success and Retention That Actually Work