Kumpulan Rumus Matematika: Jawaban untuk Soal Menantang

Kalau kamu pernah duduk di bangku sekolah dan merasa “nyangkut” di soal matematika, yakin deh—kamu nggak sendirian. Saya juga sering mengalaminya. Tapi satu hal yang selalu menyelamatkan saya adalah: Rumus Matematika. Yap, rumus itu seperti kunci jawaban tersembunyi. Begitu kita ngerti cara pakainya, soal sesulit apa pun bisa kita bongkar.

Dalam artikel ini, saya akan membagikan berbagai rumus matematika penting dari dasar hingga tingkat lanjut, beserta tips penggunaannya dan insight menarik dari sejarah rumus-rumus tersebut. Yuk, kita mulai perjalanan menyenangkan ini!

Apa Itu Rumus Matematika dan Mengapa Penting Dikuasai

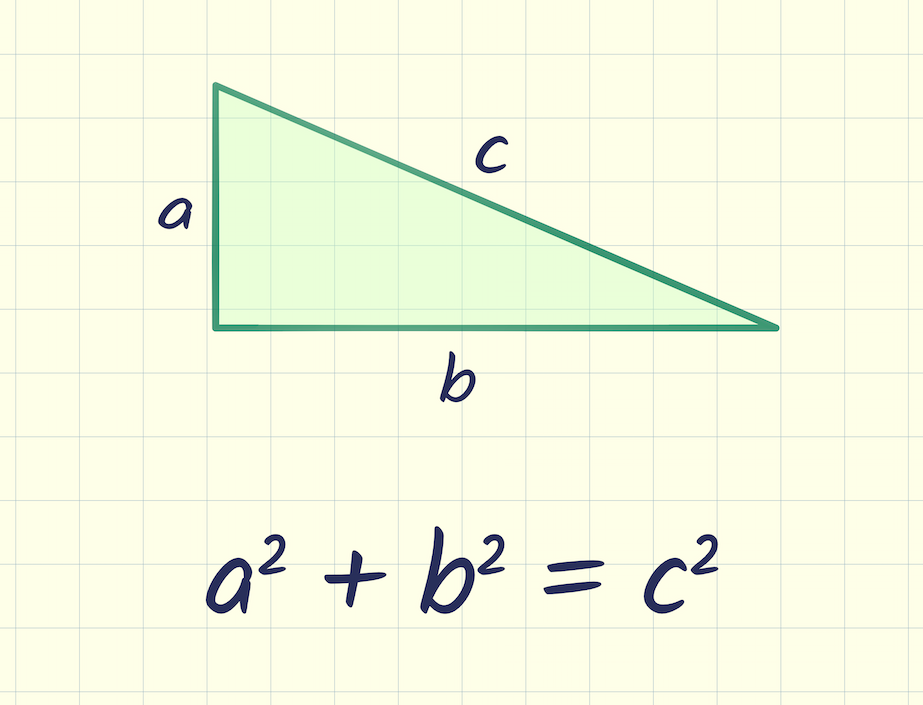
Rumus matematika adalah persamaan atau hubungan simbolik yang digunakan untuk menyelesaikan masalah. Ibarat alat tukang, rumus membantu kita mengukur, menghitung, membandingkan, dan memprediksi.

Menguasai rumus:

• Mempercepat penyelesaian soal

• Membantu berpikir logis dan sistematis

• Menjadi dasar dalam ilmu lain seperti fisika, ekonomi, bahkan coding

Saya pribadi dulu sering pakai kartu catatan kecil berisi kumpulan rumus sebelum ujian. Dan ternyata, menghafal rumus saja nggak cukup—yang penting itu tahu kapan dan bagaimana menggunakannya.

Kumpulan Rumus Matematika Dasar hingga Lanjutan

Berikut beberapa rumus dasar yang wajib kamu hafal:

1. Rumus Perkalian dan Pembagian

• Perkalian: $a\times b=b\times a$

• Pembagian: ab=c⇒a=b×c\frac{a}{b} = c \Rightarrow a = b \times cba​=c⇒a=b×c

2. Rumus Bangun Datar

• Luas Persegi: $L=s\times s$

• Luas Segitiga: L=12×a×tL = \frac{1}{2} \times a \times tL=21​×a×t

• Luas Lingkaran: L=πr2L = \pi r^2L=πr2

• Keliling Lingkaran: $K=2\pi r$

3. Rumus Bangun Ruang

• Volume Kubus: V=s3V = s^3V=s3

• Volume Balok: $V=p\times l\times t$

• Volume Tabung: V=πr2tV = \pi r^2 tV=πr2t

4. Rumus Aritmetika

• Deret aritmetika: $Un=a+(n-1)\times b$

• Jumlah n suku: Sn=n2×(2a+(n−1)b)Sn = \frac{n}{2} \times (2a + (n-1)b)Sn=2n​×(2a+(n−1)b)

5. Rumus Geometri

• Deret geometri: Un=a×rn−1Un = a \times r^{n-1}Un=a×rn−1

• Jumlah n suku: Sn=a×rn−1r−1Sn = a \times \frac{r^n – 1}{r – 1}Sn=a×r−1rn−1​ (untuk r≠1r \neq 1r=1)

Rumus Matematika SMA: Aljabar, Trigonometri, Kalkulus, dan Statistik

Aljabar

• Pemfaktoran: ax2+bx+c=(x−x1)(x−x2)ax^2 + bx + c = (x – x_1)(x – x_2)ax2+bx+c=(x−x1​)(x−x2​)

• Persamaan kuadrat: x=−b±b2−4ac2ax = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}x=2a−b±b2−4ac​​

Trigonometri

• Identitas dasar: sin⁡2x+cos⁡2x=1\sin^2 x + \cos^2 x = 1sin2x+cos2x=1

• tan⁡x=sin⁡xcos⁡x\tan x = \frac{\sin x}{\cos x}tanx=cosxsinx​

• Sudut rangkap: $\sin 2x=2\sin x\cos x$

Kalkulus

• Turunan dasar: ddxxn=nxn−1\frac{d}{dx} x^n = nx^{n-1}dxd​xn=nxn−1

• Integral dasar: ∫xndx=xn+1n+1+C\int x^n dx = \frac{x^{n+1}}{n+1} + C∫xndx=n+1xn+1​+C

Statistik

• Mean: xˉ=∑xn\bar{x} = \frac{\sum x}{n}xˉ=n∑x​

• Median: data tengah setelah diurutkan

• Modus: data yang paling sering muncul

Rumus yang Berisi Beberapa Operator Matematika Disebut Ekspresi Matematika

Kamu pasti sering lihat gabungan tanda tambah, kali, pangkat, dan kurung dalam satu baris. Nah, itu disebut ekspresi matematika.

Contohnya: 3×2+5x−23x^2 + 5x – 23x2+5x−2

Ekspresi seperti ini sangat penting dalam aljabar dan pemrograman karena menunjukkan urutan operasi. Jangan lupa aturan:

• Kerjakan tanda kurung dulu

• Lanjut perkalian/pembagian

• Terakhir penjumlahan/pengurangan

Aturan pengetahuan ini disebut PEMDAS (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction) di luar negeri.

Cara Menulis Rumus Matematika di Word dengan Mudah dan Rapi

Saya sering bikin catatan atau soal latihan di Word, dan ini tipsnya biar rapi:

1. Gunakan fitur “Equation”

• Tekan Alt + =, akan muncul kotak Equation

• Ketik rumus menggunakan simbol atau LaTeX (jika aktif)

2. Shortcut umum:

• Kuadrat: x^2

• Pecahan: \frac{a}{b}

• Akar: \sqrt{x}

3. Pakai menu Insert > Equation untuk akses simbol lengkap

Word versi terbaru makin mendukung matematika, bahkan kamu bisa menulis dengan tangan di layar sentuh, dan langsung diubah jadi teks!

Siapa Penemu Rumus Matematika? Jejak Tokoh-Tokoh Penting dalam Sejarah

Rumus-rumus matematika yang kita pakai hari ini tidak muncul begitu saja. Banyak ilmuwan besar yang menyumbangkan pikirannya:

– Pythagoras

Penemu rumus segitiga siku-siku a2+b2=c2a^2 + b^2 = c^2a2+b2=c2

– Euclid

Bapak geometri; penulis buku “Elements”

– Isaac Newton & Leibniz

Pengembang kalkulus modern

– Carl Friedrich Gauss

Pakar teori bilangan dan statistik

– Blaise Pascal

Penemu segitiga Pascal dan teori probabilitas

Saya pribadi suka baca kisah mereka karena membuktikan bahwa matematika berkembang dari rasa penasaran dan logika yang kuat. Bukan karena jenius dari lahir, tapi karena konsistensi dan dedikasi.

Rumus Matematika yang Belum Terpecahkan dan Masih Jadi Misteri Dunia

Ternyata, nggak semua rumus punya jawaban! Masih banyak persoalan matematika yang belum terpecahkan.

Contoh:

• Hipotesis Riemann: tentang distribusi bilangan prima

• P vs NP Problem: menyangkut efisiensi algoritma komputer

• Collatz Conjecture: teka-teki bilangan bulat sederhana

Beberapa soal ini bahkan menurut Wikipedia masuk daftar 7 Millennium Prize Problems, dan masing-masing bernilai 1 juta dolar AS kalau kamu bisa pecahkan!

Ini bukti bahwa matematika masih terus tumbuh. Bahkan hari ini, mungkin kamu sedang belajar rumus yang kelak bisa kamu kembangkan jadi terobosan dunia.

Kesimpulan: Pahami Rumus, Pecahkan Soal, Kuasai Matematika

Buat sebagian orang, rumus mungkin terasa menakutkan. Tapi percayalah, mereka bukan musuh. Justru mereka adalah alat bantu untuk berpikir logis dan efisien.

Saya sendiri makin suka matematika setelah mengerti rumus-rumusnya. Rasanya kayak punya “kunci rahasia” yang bisa membuka segala soal.

Jadi, mulai sekarang, jangan cuma hafal rumus. Pahami cara kerjanya, praktikkan dalam soal, dan coba cari tahu kisah di baliknya. Siapa tahu, kamu bisa jadi penemu rumus selanjutnya!

Programming dari masa muda, wajib tahu tentang: Belajar Coding 101: Cara Belajar Programming Tanpa Bingung