Faktorisasi prima adalah proses menguraikan suatu bilangan menjadi perkalian dari bilangan-bilangan prima. Metode ini merupakan dasar penting dalam matematika karena membantu menyederhanakan operasi matematika, mengenali pola angka, hingga diaplikasikan dalam dunia komputer dan kriptografi.
Apa Itu Faktorisasi Prima?
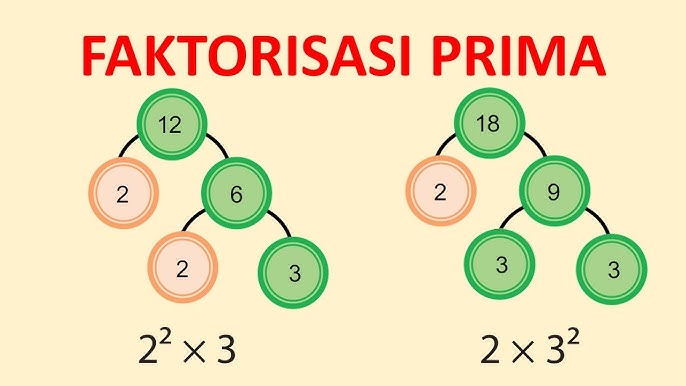
Faktorisasi prima adalah bentuk penyajian suatu bilangan sebagai hasil kali dari bilangan-bilangan prima. Misalnya, 12 dapat difaktorkan menjadi 2 × 2 × 3. Dalam hal ini, 2 dan 3 adalah bilangan prima.
Bilangan prima adalah bilangan yang hanya memiliki dua faktor, yaitu satu dan dirinya sendiri. Contohnya adalah 2, 3, 5, 7, 11, 13, dan seterusnya.
Menurut Wikipedia, bilangan prima merupakan fondasi utama dalam sistem bilangan dan merupakan bagian penting dari teori bilangan.
Mengapa Faktorisasi Prima Penting?
Faktorisasi prima bukan sekadar alat bantu dalam pelajaran matematika, tapi juga berfungsi dalam:
- Menyederhanakan pecahan
- Menentukan KPK (Kelipatan Persekutuan Terkecil) dan FPB (Faktor Persekutuan Terbesar)
- Menemukan pola dan sifat bilangan
- Kriptografi dan keamanan komputer
Langkah Mudah Melakukan Faktorisasi Prima
Berikut adalah langkah-langkah mudah untuk memfaktorkan bilangan besar:
- Mulai dari Bilangan Prima Terkecil Gunakan bilangan prima terkecil, yaitu 2. Jika tidak bisa dibagi 2, lanjutkan ke 3, lalu 5, dan seterusnya.
- Gunakan Pembagian Bertingkat Bagi bilangan dengan bilangan prima dan tulis hasilnya. Ulangi proses sampai hasilnya 1.
- Catat Semua Faktor Prima Semua bilangan pembagi yang digunakan disebut faktor prima dari bilangan tersebut.
Contoh Faktorisasi Prima
- Contoh 1: 60 60 ÷ 2 = 30 30 ÷ 2 = 15 15 ÷ 3 = 5 5 ÷ 5 = 1 Maka, faktorisasiprimanya adalah 2 × 2 × 3 × 5
- Contoh 2: 84 84 ÷ 2 = 42 42 ÷ 2 = 21 21 ÷ 3 = 7 7 ÷ 7 = 1 Faktorisasiprimanya adalah 2 × 2 × 3 × 7
Alat Bantu: Pohon Faktor
Pohon faktor adalah alat visual yang membantu menyusun faktorisasi prima dalam bentuk cabang-cabang seperti pohon. Setiap percabangan mewakili pembagian bilangan menjadi dua bilangan, hingga semuanya menjadi bilangan prima.
Contoh: 120 /
12 10 / \ /
2 6 2 5 /
2 3
Hasil: 2 × 2 × 2 × 3 × 5
Aplikasi Faktorisasi Prima dalam Kehidupan
Faktorisasi prima bukan hanya untuk pelajaran sekolah. Di dunia nyata, ia digunakan dalam:
- Kriptografi: Dalam algoritma enkripsi seperti RSA
- Teknik komputer: Untuk mengelompokkan data
- Ekonomi: Dalam perhitungan efisiensi produksi atau pembagian sumber daya
Sebagai bentuk Pengetahuan yang aplikatif, faktorisasi prima mendasari banyak teknologi pengamanan data modern.
Tips dan Trik Mempermudah Faktorisasi
- Hafalkan bilangan prima hingga 100
- Gunakan metode tabel pembagian jika angka terlalu besar
- Gunakan kalkulator bilangan prima online
Kesalahan Umum dalam Faktorisasi
- Menganggap 1 sebagai bilangan prima (padahal bukan)
- Melewatkan faktor prima kecil seperti 2 atau 3
- Tidak menyusun hasil kali dalam urutan dari kecil ke besar
Jenis-Jenis Bilangan dalam Faktorisasi
- Bilangan Prima: hanya bisa dibagi 1 dan dirinya sendiri
- Bilangan Komposit: bisa dibagi dengan bilangan lain selain 1 dan dirinya sendiri
Latihan Soal Faktorisasi Prima
- Faktorkan 45
- Faktorkan 100
- Faktorkan 210
Jawaban:
- 3 × 3 × 5
- 2 × 2 × 5 × 5
- 2 × 3 × 5 × 7
Faktorisasi Prima dan KPK serta FPB
KPK dan FPB bisa dihitung lebih mudah jika sudah melakukan faktorisasi prima.
- KPK: Ambil semua faktor prima yang muncul dengan pangkat tertinggi
-
FPB: Pilihlah faktor prima yang identik dari kedua bilangan, lalu ambil nilai pangkat terendahnya sebagai hasil yang paling efisien dan cerdas
Contoh:
- A = 18 = 2 × 3 × 3
- B = 24 = 2 × 2 × 2 × 3
FPB = 2 × 3 = 6 KPK = 2 × 2 × 2 × 3 × 3 = 72
Faktorisasi Prima untuk Angka Besar
Gunakan metode pembagian bertingkat atau pohon faktor untuk angka besar. Jika tidak memungkinkan secara manual, gunakan aplikasi kalkulator atau program seperti Python untuk membantu.
Contoh faktorisasi 315: 315 ÷ 3 = 105 105 ÷ 3 = 35 35 ÷ 5 = 7 7 ÷ 7 = 1 Maka hasilnya adalah 3 × 3 × 5 × 7
Kesimpulan
Faktorisasi prima adalah alat penting dalam matematika dan kehidupan sehari-hari. Dengan memahami konsep dan langkah-langkahnya, angka besar dapat dipecah dengan mudah menjadi bagian terkecilnya yang disebut bilangan prima. Ini tidak hanya meningkatkan keterampilan berhitung tetapi juga membuka pintu pada aplikasi dunia nyata yang lebih kompleks.
Bacalah artikel lainnya: Jari Tangan Mengkerut: Tanda Cerdas Tubuh Saat Basah


