Saya masih ingat betul saat pertama kali belajar Teorema Pythagoras di kelas 8. Guru matematika saya waktu itu, Bu Reni, menulis rumus legendaris a² + b² = c² di papan tulis dan berkata, “Rumus ini akan menyelamatkan kalian seumur hidup.” Jujur, waktu itu saya cuma bisa cengar-cengir. Masa iya sih segitiga bisa ‘menyelamatkan’ hidup?
Tapi ternyata benar. Seiring waktu, teorema ini jadi salah satu alat paling praktis yang sering saya gunakan. Dari ngukur kabel antena, merancang rak dinding yang presisi, sampai main game puzzle yang melibatkan sudut dan jarak—semua ujung-ujungnya pakai rumus ini. Bahkan waktu bantu sepupu renovasi rumah, saya pakai Pythagoras buat pastikan sudut antara dinding dan lantai itu benar-benar siku-siku.
Makanya, artikel ini saya tulis bukan cuma untuk kasih tahu rumusnya, tapi juga gimana caranya kamu bisa cepat dan akurat menemukan panjang sisi segitiga dalam berbagai situasi. Saya juga bakal cerita pengalaman, kesalahan umum, dan tips cepat yang bisa kamu langsung praktikkan.
Apa Itu Teorema Pythagoras dan Kenapa Penting Banget

Oke, sebelum lanjut, mari kita ulang sebentar.
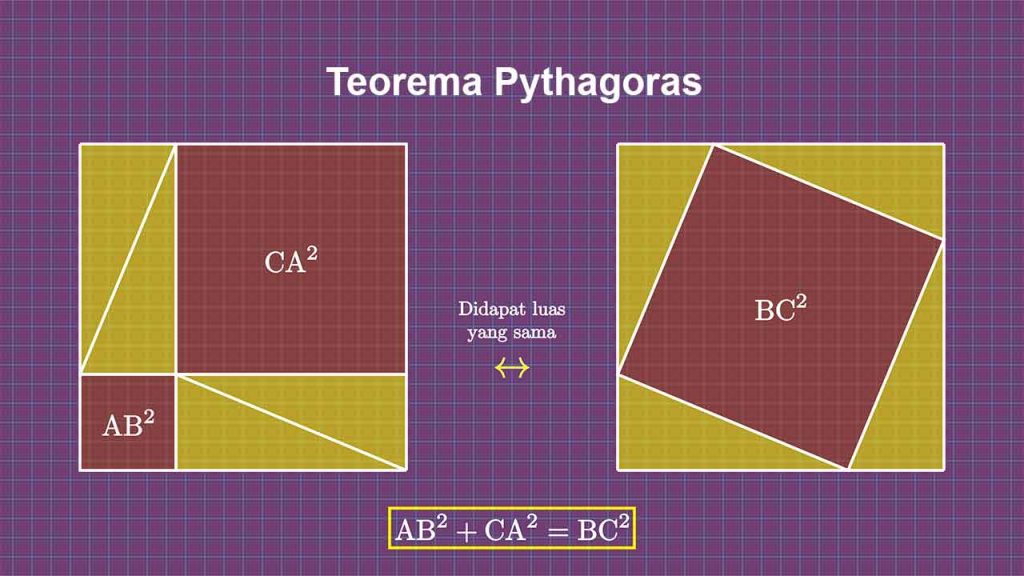
Teorema Pythagoras Matematika berbunyi:
“Di dalam segitiga siku-siku, total kuadrat panjang sisi miring disebut juga hipotenusa harus sama dengan jumlah kuadrat dari kedua sisi lainnya.”
Atau dalam rumus:
a² + b² = c²
dengan c adalah sisi miring (yang menghadap sudut 90°), sedangkan a dan b adalah sisi siku-siku.
Contoh sederhana:
Kalau kamu punya segitiga dengan sisi a = 3 cm dan b = 4 cm, maka:
c² = 3² + 4² = 9 + 16 = 25 → c = √25 = 5 cm
Saya suka menyebutnya “rumus segitiga instan.” Praktis banget dan bisa langsung dipakai bahkan tanpa kalkulator kalau angkanya pas.
Cara Cepat Menghitung Panjang Sisi Segitiga
Kalau kamu udah hafal kuadrat angka 1 sampai 20, Teorema Pythagoras ini bisa kamu pakai seperti kalkulator mini di otak.
Berikut tiga skenario pengetahuan utama:
1. Mencari Hipotenusa (sisi miring)
Gunakan rumus:
c = √(a² + b²)
Contoh:
a = 6, b = 8 → c = √(36 + 64) = √100 = 10
2. Mencari Sisi Tegak (sisi yang lain, jika diketahui hipotenusa dan satu sisi)
Rumus:
a = √(c² – b²)
Contoh:
c = 13, b = 5 → a = √(169 – 25) = √144 = 12
3. Gunakan Tabel Pythagorean Triple
Beberapa angka yang sering muncul sebagai hasil Pythagoras disebut Pythagorean triple, contohnya:
-
3, 4, 5
-
5, 12, 13
-
6, 8, 10
-
7, 24, 25
-
9, 12, 15
Dengan menghafal pola ini, kamu bisa jawab soal hitungan cepat di ujian atau olimpiade matematika tanpa ribet.
Kesalahan Umum yang Sering Saya Temui (dan Dulu Saya Lakukan Juga)
Saya akui, dulu saya sempat sering salah pakai rumus ini. Beberapa kesalahan umum:
-
Keliru urutan angka: Kadang malah kuadrat sisi miring dikurang sisi pendek, padahal kebalik.
-
Lupa pastikan segitiganya siku-siku: Teorema ini hanya berlaku untuk segitiga siku-siku.
-
Langsung ngitung tanpa cek apakah masuk akal: Misalnya dapat panjang sisi 15 cm padahal sisi lainnya cuma 3 cm dan 4 cm—jelas mustahil.
-
Keliru pakai rumus untuk diagonal persegi atau bidang miring tanpa gambar jelas.
Tips saya: selalu gambar sketsanya dulu. Nggak harus rapi, tapi cukup buat bantu otakmu memvisualisasikan posisi sisi-sisinya.
Penerapan Teorema Pythagoras di Kehidupan Nyata
Banyak orang mikir ini cuma rumus sekolah, padahal sebaliknya. Saya pribadi sudah pakai teorema ini dalam berbagai hal:
-
Nentuin panjang tangga biar bisa sampai ke atap rumah (dengan tinggi dinding dan jarak pijakan).
-
Mengukur diagonal meja atau TV.
-
Mengecek apakah ruangan berbentuk siku-siku pas renovasi.
-
Membuat desain grafis atau furniture dengan ukuran simetris.
-
Di dunia arsitektur dan teknik sipil, rumus ini digunakan tiap hari.
Bahkan di dunia penerbangan, teorema ini dipakai untuk menghitung jarak terpendek antar dua titik koordinat.
Dan ya, buat kamu yang main game atau coding, sering banget pake rumus ini buat ngitung jarak antar dua titik, terutama dalam 2D space. Di dunia komputer, ini disebut Euclidean Distance—dan dasarnya tetap Pythagoras.
Trik Cepat Menghitung Tanpa Kalkulator
Berikut beberapa trik saya:
-
Hafalkan kuadrat 1–20 (1, 4, 9, 16, 25… sampai 400)
-
Kalau nemu angka yang bukan kuadrat sempurna, gunakan perkiraan akar. Misalnya √50 mendekati √49 = 7, jadi hasilnya kira-kira 7,1.
-
Untuk sisi miring yang besar, gunakan rumus Pythagoras versi singkat:
Contoh: a = 9, b = 12 → c² = 81 + 144 = 225 → c = 15
Kamu juga bisa coba latihan soal di situs seperti Khan Academy untuk dapetin pemahaman visual yang lebih kuat, terutama kalau kamu tipe pembelajar visual kayak saya.
Teorema Pythagoras di Bangun Ruang dan Koordinat
Ternyata, rumus ini bukan cuma buat segitiga di kertas. Kita juga bisa pakai untuk:
-
Menghitung diagonal kubus atau balok
Misalnya diagonal ruang = √(panjang² + lebar² + tinggi²) -
Sistem koordinat (x,y)
Jarak antara dua titik = √((x₂ – x₁)² + (y₂ – y₁)²)
Saya dulu suka pusing waktu belajar koordinat kartesius sampai akhirnya sadar: rumusnya cuma perlu Pythagoras ditambah koordinat. Sejak itu, jadi lebih gampang memahami geometri analitik dan persamaan garis lurus.
Variasi Lain: Teorema Pythagoras Terbalik
Kadang soal ujian juga minta kita cek apakah sebuah segitiga adalah segitiga siku-siku.
Caranya:
-
Cek apakah a² + b² = c² Kalau iya, maka itu segitiga siku-siku.
Contoh:
a = 8, b = 15, c = 17
→ 8² + 15² = 64 + 225 = 289
→ √289 = 17 → benar, berarti ini segitiga siku-siku.
Teorema ini juga penting banget kalau kamu suka ikut lomba matematika atau ujian kompetitif. Cepat, jelas, dan powerful.
Pythagoras Bukan Cuma Matematika, Tapi Filosofi Hidup
Salah satu hal menarik waktu saya makin mendalami Pythagoras adalah bahwa dia bukan cuma matematikawan, tapi juga seorang filsuf. Dia percaya bahwa dunia bisa dijelaskan melalui angka dan proporsi.
Bahkan, banyak prinsip harmonisasi dalam musik, arsitektur klasik, dan seni rupa berasal dari pemikiran pythagorean—termasuk konsep “keindahan dari simetri”.
Jadi sebenarnya, belajar Pythagoras itu bukan cuma soal angka, tapi juga cara berpikir yang logis, runtut, dan presisi.
Tips Belajar dan Mengajarkan Pythagoras dengan Menyenangkan
Buat kamu yang guru atau pengajar, berikut cara saya menjelaskan konsep ini ke adik saya yang waktu itu masih kelas 7:
-
Gunakan benda nyata: seperti penggaris, kertas lipat, atau kardus.
-
Tunjukkan lewat permainan: bikin teka-teki “cari panjang sisi segitiga hilang”.
-
Pakai visual atau video animasi.
-
Beri contoh real: seperti ukuran lapangan, tangga rumah, atau jarak antar titik di peta.
Semakin nyata, semakin gampang dipahami. Teorema ini sebenarnya sederhana, tapi powerful banget.
Penutup: Jangan Takut Sama Matematika
Teorema Pythagoras bisa jadi pintu masuk untuk mencintai matematika. Dari hanya sebaris rumus, kita bisa eksplorasi bentuk, ukuran, ruang, dan bahkan filosofi logika.
Saya sendiri awalnya cuma hafal karena PR. Tapi sekarang, saya bisa bilang: ini salah satu rumus paling berguna dan menyenangkan yang pernah saya pelajari.
Kalau kamu belum terlalu paham, nggak apa-apa. Baca ulang, gambar sketsanya, dan coba soal sederhana. Lama-lama, kamu pasti bisa menggunakannya seperti reflek.
Dan yang terpenting: jangan cuma hafal, tapi pahami kenapa rumus ini bekerja.
Garis dan panah yang mudah dikerjakan asal dipahami, cek juga: Vektor: Arah dan Besar Gaya dalam Matematika